Calculadora de Pentagono (regular e irregular)
Como Calcular a Área de um Pentágono Regular
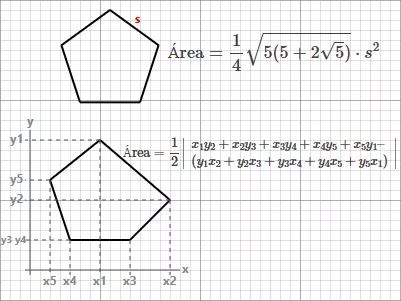
Para calcular a área de um pentágono regular, que tem cinco lados iguais, você pode usar a seguinte fórmula, que depende apenas do comprimento do lado \( s \):
\[ \text{Área} = \frac{1}{4} \times \sqrt{5(5 + 2\sqrt{5})} \times s^2 \]Passo a Passo do Cálculo:
- Calcule a constante:
- \( \sqrt{5} \approx 2,2361 \).
- \( 5 + 2 \times \sqrt{5} = 5 + 4,4721 = 9,4721 \).
- \( 5 \times 9,4721 = 47,3607 \).
- \( \sqrt{47,3607} \approx 6,8819 \).
- Constante final: \( \frac{6,8819}{4} = 1,7205 \).
- Calcule a área:
- Eleve o lado ao quadrado: \( s^2 \).
- Multiplique pela constante: \( \text{Área} = 1,7205 \times s^2 \).
Exemplo Prático:
Se o lado do pentágono mede 5 cm:
- Calcule \( s^2 \):
- \( 5^2 = 25 \).
- Calcule a área:
- \( \text{Área} = 1,7205 \times 25 = 43,01 \).
Resultado: A área do pentágono é 43,01 cm².
Por Que Essa Fórmula Funciona?
A fórmula vem da divisão do pentágono em cinco triângulos isósceles iguais. Cada triângulo tem um ângulo central de 72 graus. Usando trigonometria, encontramos uma expressão que relaciona a área ao comprimento do lado.
Importante Sobre as Unidades:
Mantenha as unidades consistentes. Se o lado está em centímetros, a área será em centímetros quadrados (\( \text{cm}^2 \)). No cálculo, selecione a unidade adequada para obter o resultado correto.
Como Calcular a Área de um Pentágono Irregular
Para calcular a área de um pentágono irregular, que tem cinco lados de diferentes comprimentos e uma forma não regular, você pode usar a fórmula do Teorema do Polígono de Shoelace, que depende das coordenadas dos vértices do pentágono:
\[ \text{Área} = \frac{1}{2} \times \left| (x_1 \cdot y_2 + x_2 \cdot y_3 + x_3 \cdot y_4 + x_4 \cdot y_5 + x_5 \cdot y_1) – (y_1 \cdot x_2 + y_2 \cdot x_3 + y_3 \cdot x_4 + y_4 \cdot x_5 + y_5 \cdot x_1) \right| \]Importante! Para resultados corretos, insira as coordenadas em ordem horário ou anti-horário.
Passo a Passo do Cálculo:
- Defina as coordenadas dos vértices:
- Identifique as coordenadas \( (x_1, y_1), (x_2, y_2), (x_3, y_3), (x_4, y_4), (x_5, y_5) \) dos vértices do pentágono.
- Substitua as coordenadas na fórmula do Shoelace:
- Insira as coordenadas na fórmula e calcule a soma e a subtração dos termos conforme descrito acima.
- Calcule a área:
- Aplique a fórmula para obter o valor da área.
Exemplo Prático:
Se as coordenadas dos vértices do pentágono forem:
- Coordenadas:
- Vértice 1: \( (1,1) \)
- Vértice 2: \( (6,1) \)
- Vértice 3: \( (8,5) \)
- Vértice 4: \( (17,10) \)
- Vértice 5: \( (3,5) \)
- Substituindo na fórmula:
- Calcule a soma e subtração dos produtos conforme a fórmula para obter a área.
- Resultado:
- A área do pentágono será 32,5 cm².

 Peter Faber
Peter Faber