Calculadora Área do Paralelogramo

por

Base:

Altura:

Unidade:

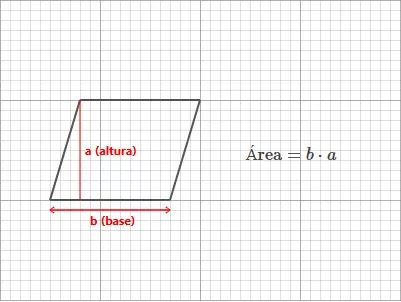
A área de um paralelogramo pode ser facilmente calculada usando sua base e altura. Mesmo que os lados sejam inclinados, o cálculo da área segue um princípio semelhante ao de um retângulo: multiplicamos a base pela altura.

Como funciona?

Pense no paralelogramo como um retângulo que foi deslocado para um lado. A fórmula para encontrar sua área é:

A geometria do paralelogramo permite visualizar isso de forma simples. Se cortarmos um triângulo da lateral do paralelogramo e o movermos para o outro lado, ele se reorganiza em um retângulo, mantendo a mesma área. Assim, basta conhecer a base e a altura para obter o resultado.

Nossa calculadora utiliza essa fórmula fundamental para fornecer resultados rapidamente. Basta inserir os valores correspondentes e obter a área com precisão. Esse é um conceito básico dentro da matemática, essencial para entender as propriedades de figuras geométricas.

Outras abordagens

Em alguns casos, podemos calcular a área de um paralelogramo usando outras abordagens. Se tivermos os lados e o ângulo entre eles, podemos aplicar a fórmula trigonométrica:

\[ \text{área} = a \times b \times \text{sen}(\text{ângulo}) \] onde

a e b representam os comprimentos dos lados adjacentes do paralelogramo.
O ângulo é o ângulo entre esses dois lados.

Além disso, se conhecermos os comprimentos das diagonais e o ângulo entre elas, podemos calcular a área com:

\[ \text{área} = \frac{1}{2} \times e \times f \times \text{sen}(\text{ângulo}) \] onde:

e e f representam os comprimentos das diagonais do paralelogramo.
O ângulo é o ângulo entre essas diagonais.

Essas abordagens podem ser úteis em situações onde a altura não é conhecida diretamente. Se precisar calcular a área de outras formas geométricas, confira também nossas ferramentas para círculos, losangos e trapézios.

Agora que você sabe como funciona, experimente calcular a área do seu paralelogramo!