Calculadora da Área do Triângulo (7 métodos)
7 métodos para calcular a área de um triângulo, dependendo do que você sabe. Cada método com sua própria calculadora.
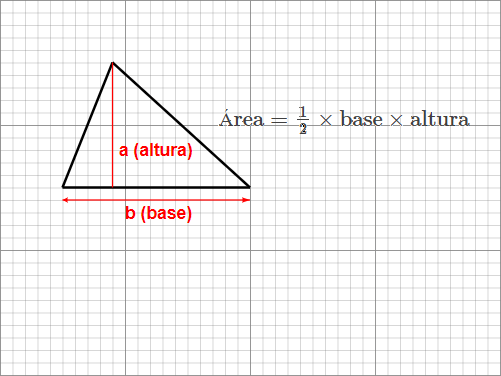
1. Base e Altura:
A fórmula mais básica para calcular a área de um triângulo usa a base e a altura do triângulo. Como um triângulo é basicamente metade de um quadrado, a fórmula fica assim:
\(\text{Área} = \frac{1}{2} \times \text{base} \times \text{altura}\)
Essa fórmula, embora também seja usada em situações práticas, é usada principalmente no ensino para fazer você entender que a área de um triângulo basicamente é metade da de um quadrado cortado ao meio.
2. Fórmula de Herão (Três lados):
\(s = \frac{a + b + c}{2}\)
\(\text{Área} = \sqrt{s(s – a)(s – b)(s – c)}\)
Funciona só com os comprimentos dos lados.
3. Trigonometria (Dois lados e o ângulo entre eles):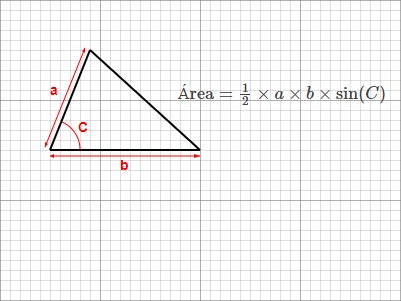
\(\text{Área} = \frac{1}{2} \times a \times b \times \sin(C)\)
Use se você conhece dois lados e o ângulo entre eles.
4. Coordenadas (Quando você conhece os vértices):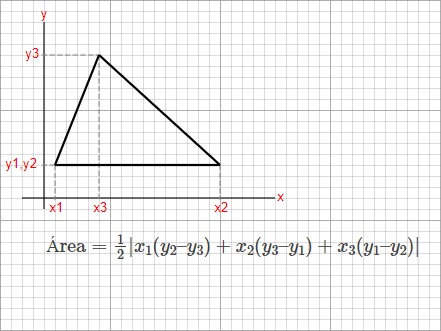
Se os vértices são \((x_1, y_1)\), \((x_2, y_2)\) e \((x_3, y_3)\):
\(\text{Área} = \frac{1}{2} \left| x_1(y_2 – y_3) + x_2(y_3 – y_1) + x_3(y_1 – y_2) \right|\)
5. Raio da Circunferência Circunscrita (circunraio) \(R\) (Com todos os lados conhecidos):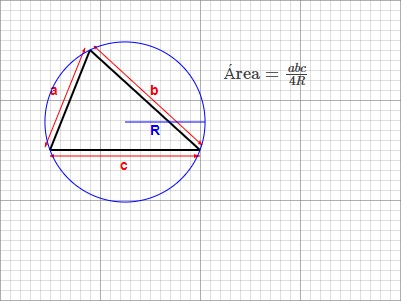
\(\text{Área} = \frac{abc}{4R}\)
Aqui, \(R\) é o circunrádio.
6. Raio da Circunferência Inscrita (Inraio) \(r\) (Usando o semiperímetro (s) e o inraio):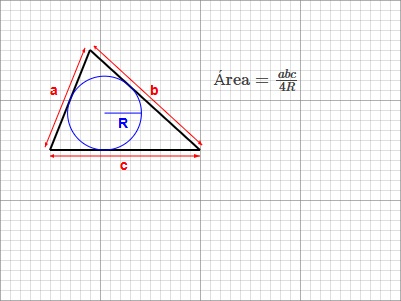
\(s = \frac{a + b + c}{2}\)
\(\text{Área} = r \times s\)
\(r\) é o inrádio, \(s\) é o semiperímetro.
7. Produto Vetorial (Se você conhece os vetores):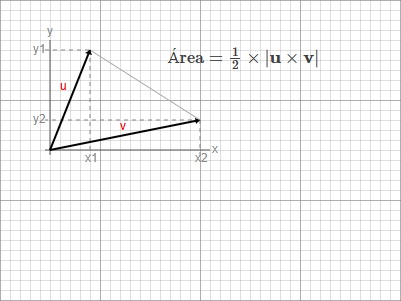
Se você tem dois vetores \(\mathbf{u}\) e \(\mathbf{v}\):
\(\text{Área} = \frac{1}{2} \times |\mathbf{u} \times \mathbf{v}|\)
Uy:
Vy:
Esses métodos cobrem diferentes casos, dependendo do que você sabe sobre o triângulo.

 Peter Faber
Peter Faber